Sorry, your browser cannot access this site
This page requires browser support (enable) JavaScript
Learn more >

Understanding gzip - Huffman coding

Base Service

publish date:Mar 7, 2022

7.9k words

37 min

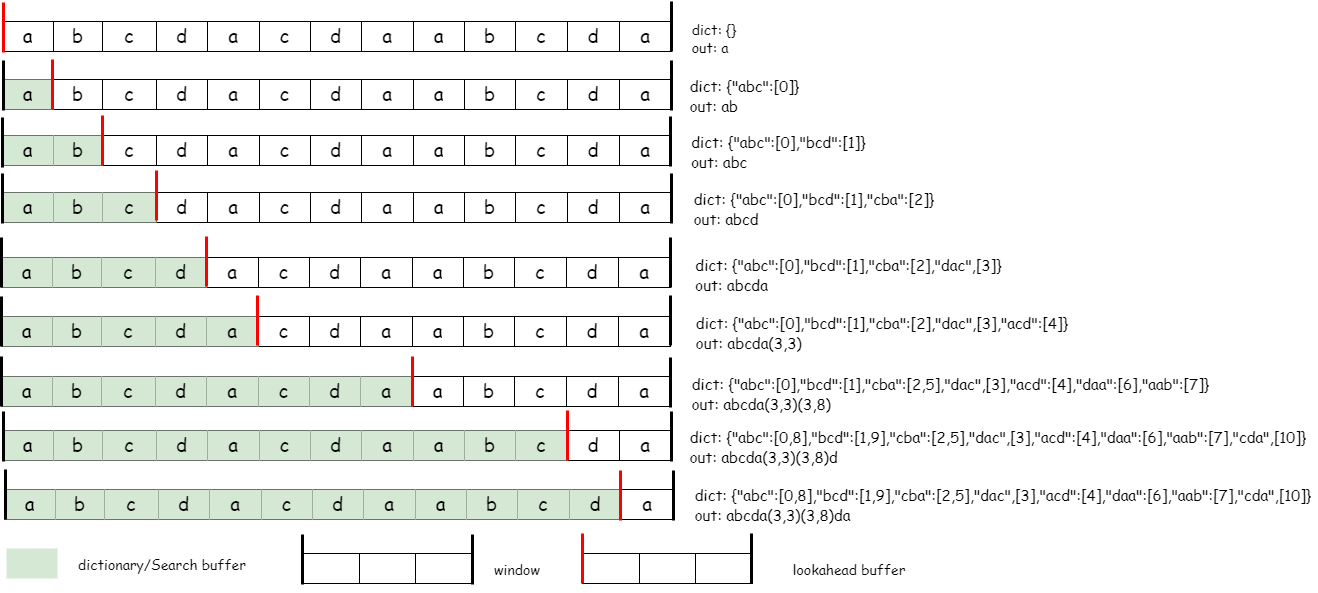
DEFLATE算法首先通过LZ77算法对数据流压缩，压缩数据流中仅包含literal、length、distance三种类型的数据。

数据是通过字符表(alphabet)中的编码表示，如ASCII编码的纯文本文件中的数据都来源于ASCII字符表。字母表中的字符在计算机中以二进制形式存储，如ASCII表中的字符A的二进制编码是长度为1字节的1000001B。DEFLATE算法定义了两张字符表编码上述三种类型的数据：literal和length使用一张字符表，distance单独一张字符表。

alphabet

literal和length使用一张285个编码(codes)的字符表。(0..255)是literal的编码，直接使用ASCII编码。length的取值范围是(3..258)，使用(257..285)编码区间，字符256代表end-of-block，DEFLATE算法的压缩数据以block形式组织，end-of-block是block的结束标识。
literal这种一一对应的编码很好理解，length的取值范围明显大于编码范围，详细看看DEFLATE算法如何编码length：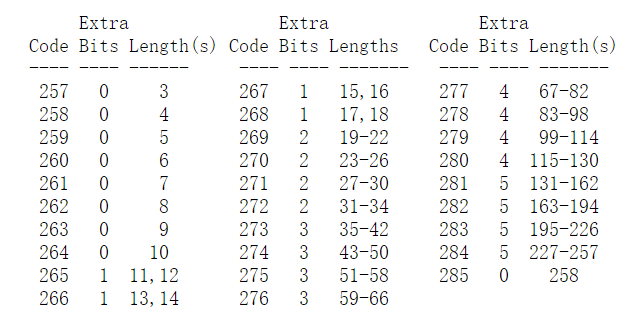

DEFLATE将length的取值从(3..258)编码到(257..285)的编码范围，因此，一些length会共用同一编码。紧随编码之后的Extra bits解决了同一编码共享的问题。以length的取值11、12为例，它们共享同一编码265，如果编码265在计算机中以3-bit的二进制编码110B存储，则length 11的二进制编码是1100B,length 12的二进制编码是1101B。literal & length字符表中，length越长，Extra bits越长；同时也意味着字符串匹配的长度越长，出现的概率越小。可见，DEFLATE算法在字符长度和计算复杂度之间做了trade off的。不过，285这个字符Extra bits长度为0，可能因为285作为DEFLATE算法规定的最大匹配长度，出现的概率也会更高。

distance的字符表如下所示，不再过多解释：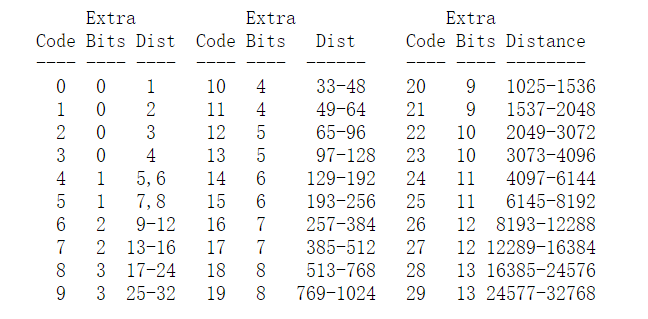

Huffman coding

字符表中的编码有两种二进制编码方式：定长(fixed-length)编码、变长(variable-length)编码。
ASCII编码是定长编码，每个字符都用长度为1字节的二进制表示。定长编码具有明确易解析的优点，每读取一个字节的数据，便可解析(decode)得到相应的字符，如读取到1字节的数据1000001B，便可解析得到字符A。
Huffman编码是变长编码的代表，基于字符实际出现的频次，出现频次高的字符的编码长度越短，反之则更长。Huffman编码要求所有编码具有prefix property：任一编码不能是另一更长编码的前缀。Huffman编码稍微复杂一些，但整体的编码长度更短。DEFLATE算法选择Huffman编码表示LZ77压缩数据。

DEFLATE算法将根据字符在LZ77编码字符流中出现的实际频次而构建的Huffman树，称为dynamic Huffman codes。dynamic Huffman codes模式下，两张字符表的字符Huffman编码预先是不确定的，而是在压缩过程中，读取LZ77压缩字符流、统计字符出现的实际频次而构建的。因此，需要将两张字符表的Huffman编码信息加入到最终的压缩数据流中，以便后续解压缩过程中的解码。fixed Huffman codes是DEFLATE算法预先定义的字符表的Huffman编码。

fixed Huffman codes

fixed Huffman codes编码模式下，literal/length字符表、distance字符表的Huffman编码都是固定的，下图是literal & length字符表的Huffman编码：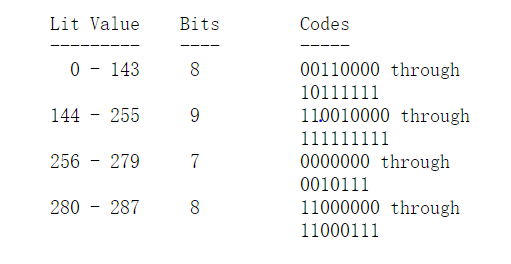

distance字符表(0..29)使用固定长度的5-bit编码(编码范围：0-31)。
到这，您可能会问fixed Huffman codes存在的意义？它并不是根据字符出现的实际频次而产生的Huffman编码，肯定不适用于任何输入数据集。
前面我们提到dynamic Huffman code还需要将两张字符表对应的Huffman编码信息加入到压缩数据流以支持后续的解压操作。那么，待压缩的数据量较小时，dynamic Huffman codes编码会额外存储的这些metadata，从而比直接使用fixed Huffman codes的编码长度更长。

dynamic Huffman codes

Run Length Encoding

dynamic Huffman codes根据字符在LZ77压缩字符流中出现的实际频次，构建Huffman树、对字符Huffman编码。直接保存字符表中每个字符的Huffman编码会极度浪费空间，这让LZ77算法的压缩变得毫无意义。DEFLATE算法约束Huffman编码：

  • 相同长度的Huffman编码在数值上是连续的，编码顺序与字符在字符表中的先后顺序保持一致
  • 长度更短的Huffman编码，其编码值更小

如下的字符表只有四个字符：ABCD，字符表中的字符顺序以及相应的Huffman编码如表所示：

Symbol Code
A 10
B 110
C 0
D 111

字符B和字符D的Huffman编码长度都是3，两者的Huffman编码是连续的，且编码顺序与字符在字符表中出现的先后顺序保持一致。按照Huffman编码长度排序：0、10、110、111。长度更短的Huffman编码，其编码值也更小。
若不考虑上述两个约定，字符表的字符在相同编码长度下，可以有多种编码，如ABCD的Huffman编码也可以是00、011、1、010。但是这种Huffman编码就未遵守上述约定。
上述两个约定的目的是，仅通过Huffman编码长度(code length)便可以确定整个Huffman树。因此，ABCD字符表的Huffman编码可以使用(2,3,1,3)来表示。gzip通过build_tree对字符表中出现的字符Huffman编码：

  1. 按照字符表中的字符出现的频次构建Huffman树
  2. 调用gen_bitlen函数获取各出现字符的编码长度，如果节点超出MAX_BITS（15），调整节点的位置
  3. 调用gen_codes函数根据Huffman树中叶子节点的编码长度，遵循DEFLATE算法的Huffman编码约束进行编码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#define HEAP_SIZE (2*L_CODES+1)
/* maximum heap size *

local int near heap[2*L_CODES+1]; /* heap used to build the Huffman trees */

/* ===========================================================================
 * Compares to subtrees, using the tree depth as tie breaker when
 * the subtrees have equal frequency. This minimizes the worst case length.
 */
#define smaller(tree, n, m) \
   (tree[n].Freq < tree[m].Freq || \
   (tree[n].Freq == tree[m].Freq && depth[n] <= depth[m]))


local void build_tree(desc)
    tree_desc near *desc; /* the tree descriptor */
{
    ct_data near *tree   = desc->dyn_tree;
    ct_data near *stree  = desc->static_tree;
    int elems            = desc->elems;
    int n, m;          /* iterate over heap elements */
    // 字符表中出现过的最大字符
    int max_code = -1; /* largest code with non zero frequency */
    int node = elems;  /* next internal node of the tree */

    heap_len = 0, heap_max = HEAP_SIZE;

    // heap数组中按照字符表中的字符顺序存储出现过的字符
    for (n = 0; n < elems; n++) {
        if (tree[n].Freq != 0) {
            heap[++heap_len] = max_code = n;
            depth[n] = 0;
        } else {
            // 忽略字符表中未出现的字符，Huffman编码长度为0，即未参与Huffman编码
            tree[n].Len = 0;
        }
    }
    ...
    desc->max_code = max_code;

    /* The elements heap[heap_len/2+1 .. heap_len] are leaves of the tree,
     * establish sub-heaps of increasing lengths:
     */
    // 将heap构建为按照字符出现频次比较的小顶堆
    for (n = heap_len/2; n >= 1; n--) pqdownheap(tree, n);

    /* Construct the Huffman tree by repeatedly combining the least two
     * frequent nodes.
     */
    do {
        pqremove(tree, n);   /* n = node of least frequency */
        m = heap[SMALLEST];  /* m = node of next least frequency */

        // m和n是Huffman树的兄弟节点
        heap[--heap_max] = n; /* keep the nodes sorted by frequency */
        heap[--heap_max] = m;

        /* Create a new node father of n and m */
        tree[node].Freq = tree[n].Freq + tree[m].Freq;
        // 同Freq的中间节点和叶子节点，按照smaller比较，叶子节点比中间节点小
        depth[node] = (uch) (MAX(depth[n], depth[m]) + 1);
        tree[n].Dad = tree[m].Dad = (ush)node;
...
        /* and insert the new node in the heap */
        heap[SMALLEST] = node++;
        pqdownheap(tree, SMALLEST);

    } while (heap_len >= 2);

    // heap[heap_max..HEAP_SIZE]包含了Huffman树的中间节点和叶子节点（字符表中的字符）
    heap[--heap_max] = heap[SMALLEST];

    /* At this point, the fields freq and dad are set. We can now
     * generate the bit lengths.
     */
    gen_bitlen((tree_desc near *)desc);

    /* The field len is now set, we can generate the bit codes */
    gen_codes ((ct_data near *)tree, max_code);
}

build_tree首先for循环调用pqdownheap完成小顶堆的堆化(heapify)操作，小顶堆中的字符是按照字符的频次排序的（详情见smaller宏）。随后的do-while循环完成Huffman树的构建。当前得到的是一棵“编码不明”的Huffman树，这里的“编码不明”指兄弟节点的左右顺序未确定，对Huffman树的叶子节点编码不是通过从根节点到叶子节点的路径所确定的。

gen_bitlen函数为了获取各出现字符的编码长度，因为最终字符的Huffman编码是根据字符的编码长度确定的。gen_bitlen函数会调整build_tree生成的Huffman树的编码过长(> MAX_BITS)节点的位置。gen_bitlen还会统计dynamic Huffman codes编码之后的长度opt_len以及fixed Huffman codes编码后的长度static_len。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
local void gen_bitlen(desc)
    tree_desc near *desc; /* the tree descriptor */
{
...
    for (bits = 0; bits <= MAX_BITS; bits++) bl_count[bits] = 0; 

    // root节点的Huffman编码长度为0，root节点是中间节点
    tree[heap[heap_max]].Len = 0; /* root of the heap */

    for (h = heap_max+1; h < HEAP_SIZE; h++) {
        n = heap[h];
        bits = tree[tree[n].Dad].Len + 1; 
        if (bits > max_length) bits = max_length, overflow++;
        tree[n].Len = (ush)bits;
        if (n > max_code) continue; /* not a leaf node */

        bl_count[bits]++;
        xbits = 0;
        if (n >= base) xbits = extra[n-base];
        f = tree[n].Freq;
        // 以dynamic Huffman codes编码的编码长度
        opt_len += (ulg)f * (bits + xbits);
        // 以fixed Huffman codes编码的编码长度
        if (stree) static_len += (ulg)f * (stree[n].Len + xbits);
    }
    if (overflow == 0) return;

    // 调整编码长度过长节点的位置
    do {
        bits = max_length-1;
        while (bl_count[bits] == 0) bits--;
        bl_count[bits]--;      /* move one leaf down the tree */
        bl_count[bits+1] += 2; /* move one overflow item as its brother */
        bl_count[max_length]--;
        /* The brother of the overflow item also moves one step up,
         * but this does not affect bl_count[max_length]
         */
        overflow -= 2;
    } while (overflow > 0);

    for (bits = max_length; bits != 0; bits--) {
        n = bl_count[bits];
        while (n != 0) {
            m = heap[--h];
            if (m > max_code) continue;
            if (tree[m].Len != (unsigned) bits) {
                // 调整overflow节点之后，根据实际编码长度重新计算dynamic Huffman codes编码长度
                opt_len += ((long)bits-(long)tree[m].Len)*(long)tree[m].Freq;
                tree[m].Len = (ush)bits;
            }
            n--;
        }
    }
}

gen_bitlen函数最后的do-while循环和for循环完成超长节点的调整，其实现主要是调整bl_count数组和调整节点m的实际编码长度tree[m].Len。可见，build_tree最初生成的Huffman树确实是一棵“编码不明”的Huffman树，即无需确定叶子节点的具体位置（无法确定是左/右子节点），只要该节点的编码长度正确即可。
下图展示了超长节点的调整过程：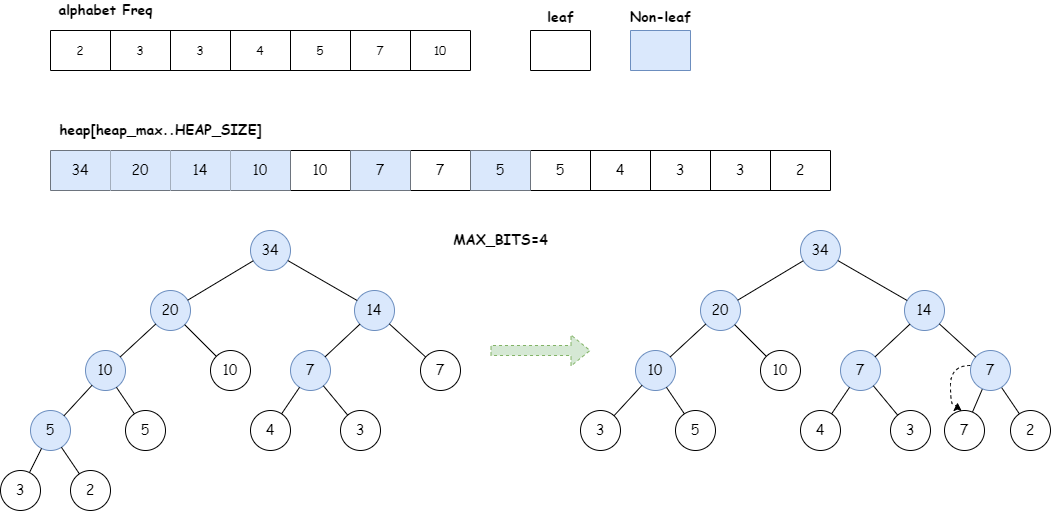

  • 字符表中字符出现的频率是(2, 3, 3, 4, 5, 7, 10)，为简化描述，后面用频次代指相应的编码
  • build_tree构建Huffman树后，节点的父子关系确定，各个节点的编码长度确定。假设当前的MAX_BITS=4，则叶子节点3、2超出了最大编码长度
  • gen_bitlen将超长编码2调整到和编码7所在同一层，那么编码7和编码2称为兄弟节点，则编码7要下移一层，原来编码7的位置变为中间节点。超长编码2的兄弟节点3，挪到其父节点的位置。因为，Huffman树的节点要么不存在子节点，要么就是两个子节点。所以移动完一个子节点，另一个子节点移动到父节点位置才符合Huffman编码，所以do-while循环是overflow -= 2。注意，前面描述的节点移动只是一个逻辑过程，代码中并未通过改变节点的Dad指代新的父节点，更不谈改变父节点的实际频次。因为后面的gen_codes仅关心节点的编码长度便可生成正确的Huffman编码，而不是实际的Huffman树长啥样，所以，我反复强调这颗Huffman树是一个“编码不明”的Huffman树

最后，gen_codes函数根据字符表的Huffman编码长度数组(code length sequence)对字符表进行Huffman编码，这个过程是RFC 1951, Section 3.2.2算法的实现。字符表中字符m的长度存储在tree[m].Len中，Huffman编码存储在tree[m].Code中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// bl_count[i]: Huffman编码长度为i的个数
// tree[i].Code: 字符表中的字符i对应的Huffman编码
// tree[i].Len: 字符表中的字符i对应的Huffman编码长度
#define MAX_BITS 15
/* All codes must not exceed MAX_BITS bits */

// max_code是字符表中频次非0的最大字符，即max_code + 1至字符表最后一个字符在数据流中出现次数都为0
local void gen_codes (tree, max_code)
    ct_data near *tree;        /* the tree to decorate */
    int max_code;              /* largest code with non zero frequency */
{
    ush next_code[MAX_BITS+1]; /* next code value for each bit length */
    ush code = 0;              /* running code value */
    int bits;                  /* bit index */
    int n;                     /* code index */

    // next_code[bits]是长度为bits的所有Huffman编码的第一个编码
    for (bits = 1; bits <= MAX_BITS; bits++) {
        // 遵守约束2，bits+1的第一个编码 会是(bits的最后一个编码+1)的2倍
        next_code[bits] = code = (code + bl_count[bits-1]) << 1;
    }    
...
    for (n = 0;  n <= max_code; n++) {
        int len = tree[n].Len;
        // 不对未出现的字符编码
        if (len == 0) continue;
        /* Now reverse the bits */
        // 遵守约束1
        tree[n].Code = bi_reverse(next_code[len]++, len);
        ...
    }    
}

可以注意到，literal/length字符表、distance字符表的Huffman编码的最大长度是15。基于上述两个约束，可以通过字符表中各个字符的编码长度(code length)来表示整个字符表的Huffman编码。实际上，DEFLATE算法通过Run Length Encoding进一步编码code length数组。如字符表的code length数组是(5, 5, 5, 5, 6, 6, 6, 6, 6, 6)，经过RLE编码后的表示是((5,4),(6,6))，即code length 5连续出现4次，code length 6连续出现6次。
DEFLATE算法将literal/length字符表、distance字符表的code length数组的REL编码保存到压缩数据流中以表示这两张字符表的Huffman编码。同样，REL编码也需要一张字符表来表示，REL编码有两种类型的数据：

  • code length：Huffman编码长度，取值范围是(0..15)
  • repeat times: code length重复次数

DEFLATE算法设计了REL编码的字符表：

code extra bits meaning
0-15 0 code lengths of 0-15
16 2 Copy the previous code length 3 - 6 times
The next 2 bits indicate repeat length
(0 = 3, … , 3 = 6)
17 3 Repeat a code length of 0 for 3 - 10 times
18 7 Repeat a code length of 0 for 11 - 138 times

举个例子，8, 16(+2 bits 11), 16(+2 bits 10)会展开成12(1 + (3 + 3) + (3 + 2))个code length为8的数据流。
code length为0表示literal/length字符表、distance字符表中的该字符未出现过，这个字符是不参与Huffman树构建的。

Huffman on RLE alphabet

至此，literal/length、distance字符表中字符的Huffman编码可以使用两个RLE序列表示。上一节也给出了RLE编码的字符表，RLE字符表中的字符也是使用Huffman编码，和对literal/length、distance字符表中的字符进行Huffman编码一样。因此，DEFLATE也要将RLE字符表的Huffman编码加入到压缩数据流，以解析literal/length、distance字符表的Huffman编码的RLE序列表示。
到这一步，DEFLATE算法貌似陷入了“无限循环”，其实不然，第一次Huffman编码，将literal/length、distance字符表中字符的Huffman编码以RLE序列表示，字符表的编码范围从(0..285)|(0..29)缩小到(0..18)。再对RLE字符表进行Huffman编码，编码范围会从(0..18)继续缩减。可见，第二次Huffman编码可以将字符表的编码范围缩短的更小，因此就没有无限“套娃”的必要了！DEFLATE算法规定对RLE字符表的字符的最大Huffman编码长度限制为7。因此，对RLE字符表进行性Huffman编码得到的code length序列的取值范围为(0..7)，DEFLATE使用固定长度的3-bit编码表示这些code length。
这里，DEFLATE算法对于RLE字符表的字符排序做了优化，RLE字符表中的字符并非按照(0..18)顺序排序，而是实际分析RLE字符表中字符出现的频率，按照出现频率从高往低排序。DEFLATE算法规定RLE字符表的字符实际顺序：(16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15)。这个优化可以缩短RLE字符表的code length数组长度，如literal/length、distance字符表的两个RLE序列中所有REL字符在REL字符表中的最大索引（max index）是REL字符13所在的位置。则2, 14, 1, 15不需要出现在RLE字符表的code length数组中，可以参考前面介绍gen_codes函数的max_code参数的意义。我只能感叹，DEFLATE算法为了极致压缩，有太多trick了！！

所以，前面提及的dynamic Huffman codes的”metadata”包含：

  • RLE字符表对应的Huffman编码，以code length数组表示
  • literal/length、distance字符表的Huffman编码，以REL序列表示

Implementation Details

  1. ct_init初始化全局变量base_length、length_code、base_dist、dist_code方便length、distance与literal/length、distance字符表中的编码进行相互转换，同时完成literal & length字符表的fixed huffman编码。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    102
    103
    104
    105
    106
    107
    108
    109
    110
    111
    112
    113
    114
    115
    116
    117
    118
    119
    120
    121
    #define LENGTH_CODES 29
    /* number of length codes, not counting the special END_BLOCK code */

    #define LITERALS  256
    /* number of literal bytes 0..255 */

    #define L_CODES (LITERALS+1+LENGTH_CODES)
    /* number of Literal or Length codes, including the END_BLOCK code */

    #define D_CODES   30
    /* number of distance codes */

    local int near extra_lbits[LENGTH_CODES] /* extra bits for each length code */
       = {0,0,0,0,0,0,0,0,1,1,1,1,2,2,2,2,3,3,3,3,4,4,4,4,5,5,5,5,0};

    local int near extra_dbits[D_CODES] /* extra bits for each distance code */
       = {0,0,0,0,1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,10,11,11,12,12,13,13};

    /* Data structure describing a single value and its code string. */
    typedef struct ct_data {
        union {
            ush  freq;       /* frequency count */
            ush  code;       /* bit string */
        } fc;
        union {
            ush  dad;        /* father node in Huffman tree */
            ush  len;        /* length of bit string */
        } dl;
    } ct_data;

    local ct_data near static_ltree[L_CODES+2];
    /* The static literal tree. Since the bit lengths are imposed, there is no
     * need for the L_CODES extra codes used during heap construction. However
     * The codes 286 and 287 are needed to build a canonical tree (see ct_init
     * below).
     */

    local ct_data near static_dtree[D_CODES];
    /* The static distance tree. (Actually a trivial tree since all codes use
     * 5 bits.)
     */

    local uch length_code[MAX_MATCH-MIN_MATCH+1];
    /* length code for each normalized match length (0 == MIN_MATCH) */

    local uch dist_code[512];
    /* distance codes. The first 256 values correspond to the distances
     * 3 .. 258, the last 256 values correspond to the top 8 bits of
     * the 15 bit distances.
     */

    local int near base_length[LENGTH_CODES];
    /* First normalized length for each code (0 = MIN_MATCH) */

    local int near base_dist[D_CODES];
    /* First normalized distance for each code (0 = distance of 1) */

    void ct_init(attr, methodp)
        ush  *attr;   /* pointer to internal file attribute */
        int  *methodp; /* pointer to compression method */
    {
    ...
        if (static_dtree[0].Len != 0) return; /* ct_init already called */

        /* Initialize the mapping length (0..255) -> length code (0..28) */
        // base_length[i]：literal/length字符表中的第i个length code表示范围的第一个length
        // length_code[i]: 长度i在literal/length字符表对应的length code的顺序
        length = 0;
        for (code = 0; code < LENGTH_CODES-1; code++) {
            base_length[code] = length;
            for (n = 0; n < (1<<extra_lbits[code]); n++) {
                length_code[length++] = (uch)code;
            }
        }
    ...
        length_code[length-1] = (uch)code;
        // dist_code[i]: 距离i属于(0..255)时,dist_code[i]表示distance字符表中的distance code，范围是(0..15)
        // 当i属于(256..511)时，每个i代表128个distance数据，如dist_code[258] = 16 dist_code[259] = 16
        // dist_code[260] = 18  dist_code[260] = 18；因为编码16、17的distance数据有128个，编码18的distance数据有256个；dist_code的256和257索引预留
        /* Initialize the mapping dist (0..32K) -> dist code (0..29) */
        dist = 0;
        for (code = 0 ; code < 16; code++) {
            base_dist[code] = dist;
            for (n = 0; n < (1<<extra_dbits[code]); n++) {
                dist_code[dist++] = (uch)code;
            }
        }
        Assert (dist == 256, "ct_init: dist != 256");
        dist >>= 7; /* from now on, all distances are divided by 128 */
        for ( ; code < D_CODES; code++) {
            base_dist[code] = dist << 7;
            for (n = 0; n < (1<<(extra_dbits[code]-7)); n++) {
                dist_code[256 + dist++] = (uch)code;
            }
        }
        Assert (dist == 256, "ct_init: 256+dist != 512");

        /* Construct the codes of the static literal tree */
        // 将literal/length字符表的fixed huffman code通过code length sequence表示
        for (bits = 0; bits <= MAX_BITS; bits++) bl_count[bits] = 0;
        n = 0;
        while (n <= 143) static_ltree[n++].Len = 8, bl_count[8]++;
        while (n <= 255) static_ltree[n++].Len = 9, bl_count[9]++;
        while (n <= 279) static_ltree[n++].Len = 7, bl_count[7]++;
        while (n <= 287) static_ltree[n++].Len = 8, bl_count[8]++;
        /* Codes 286 and 287 do not exist, but we must include them in the
         * tree construction to get a canonical Huffman tree (longest code
         * all ones)
         */
        // 对literal/length字符表进行Huffman编码
        gen_codes((ct_data near *)static_ltree, L_CODES+1);

        // distance字符表的固定编码使用5-bit长度的顺序编码
        for (n = 0; n < D_CODES; n++) {
            static_dtree[n].Len = 5;
            static_dtree[n].Code = bi_reverse(n, 5);
        }
        
        /* Initialize the first block of the first file: */
        init_block();
    }
  2. ct_tally统计literal & length字符表中literal、length字符出现的频率，并将literal、length保存到l_buf中；统计distance字符表中的distance字符出现的频率，并将distance保存到d_buf中，其中一个buffer满时，将两个buffer中保存的LZ77压缩字符流组织成block压缩块。l_buf、d_buf保存literal、length、distance的方式在随后介绍compress_block函数会详细讲解。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    local ct_data near dyn_ltree[HEAP_SIZE];   /* literal and length tree */
    local ct_data near dyn_dtree[2*D_CODES+1]; /* distance tree */

    // 完成distance到distance字符表中的code映射
    #define d_code(dist) \
       ((dist) < 256 ? dist_code[dist] : dist_code[256+((dist)>>7)])
    /* Mapping from a distance to a distance code. dist is the distance - 1 and
     * must not have side effects. dist_code[256] and dist_code[257] are never
     * used.
     */

    // 编码literal: dist = 0, lc = literal
    // 编码<length, distance>: dist = distance, lc = length - MIN_MATCH
    int ct_tally (dist, lc)
        int dist;  /* distance of matched string */
        int lc;    /* match length-MIN_MATCH or unmatched char (if dist==0) */
    {
        // l_buf保存literal、length
        l_buf[last_lit++] = (uch)lc;
        if (dist == 0) { 
            /* lc is the unmatched char */
            // 统计literal/length字符表中相应的literal code出现频率
            dyn_ltree[lc].Freq++;
        } else {
            /* Here, lc is the match length - MIN_MATCH */
            dist--;             /* dist = match distance - 1 */
            Assert((ush)dist < (ush)MAX_DIST &&
                   (ush)lc <= (ush)(MAX_MATCH-MIN_MATCH) &&
                   (ush)d_code(dist) < (ush)D_CODES,  "ct_tally: bad match");

            // 统计literal/length字符表中相应的length code出现频率
            dyn_ltree[length_code[lc]+LITERALS+1].Freq++;
            // 统计distance字符表中相应的distance code出现频率
            dyn_dtree[d_code(dist)].Freq++;

            // d_buf保存distance
            d_buf[last_dist++] = (ush)dist;
            flags |= flag_bit;
        }    
        flag_bit <<= 1;

        /* Output the flags if they fill a byte: */
        if ((last_lit & 7) == 0) { 
            flag_buf[last_flags++] = flags;
            flags = 0, flag_bit = 1; 
        }    

        ...
        return (last_lit == LIT_BUFSIZE-1 || last_dist == DIST_BUFSIZE);
    }
  3. flush_block完成整个block的编码
  • 调用build_tree完成对literal & length字符表、distance字符表Huffman编码。
  • 调用build_bl_tree对literal & length字符表、distance字符表的Huffman编码的REL表示所在的REL字符表进行Huffman编码
  • 根据情况判断是直接将数据未经压缩输出还是以不同type的block形式输出
    • no compression block：调用copy_block直接输出数据
    • compressed with fixed Huffman codes：compress_block根据static Huffman tree对LZ77压缩数据进行Huffman编码
    • compressed with dynamic Huffman codes：send_all_trees将REL字符表的code length sequence、literal & length字符表、distance字符表的Huffman编码的REL序列输出；compress_block根据dynamic Huffman tree对LZ77压缩数据编码
  • 调用init_block初始化下一block

DEFLATE算法规定block有3bit的头部信息：

  • first bit: BFINAL(last block set)
  • next 2 bits: BTYPE

BTYPE表示block的压缩类型：

  • 00 - no compression
  • 01 - compressed with fixed Huffman codes
  • 10 - compressed with dynamic Huffman codes
  • 11 - reserved (error)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#define FLUSH_BLOCK(eof) \
   flush_block(block_start >= 0L ? (char*)&window[(unsigned)block_start] : \
                (char*)NULL, (long)strstart - block_start, flush-1, (eof))

off_t flush_block(buf, stored_len, pad, eof)
    char *buf;        /* input block, or NULL if too old */
    ulg stored_len;   /* length of input block */
    int pad;          /* pad output to byte boundary */
    int eof;          /* true if this is the last block for a file */
{
    ulg opt_lenb, static_lenb; /* opt_len and static_len in bytes */
    int max_blindex;  /* index of last bit length code of non zero freq */

    flag_buf[last_flags] = flags; /* Save the flags for the last 8 items */

     /* Check if the file is ascii or binary */
    if (*file_type == (ush)UNKNOWN) set_file_type();

    /* Construct the literal and distance trees */
    build_tree((tree_desc near *)(&l_desc));
    build_tree((tree_desc near *)(&d_desc));

    // 对literal|length字符表以及distance字符表的REL编码的REL字符表进行Huffman编码，max_blindex是出现过自大的REL字符的索引
    max_blindex = build_bl_tree();

    // 3 header bits + 7 = (8 - 1)，(x + 7) >> 3表示容纳x bit需要多少字节
    opt_lenb = (opt_len+3+7)>>3;
    static_lenb = (static_len+3+7)>>3;
    input_len += stored_len; /* for debugging only */

    if (static_lenb <= opt_lenb) opt_lenb = static_lenb;

    /* If compression failed and this is the first and last block,
     * and if we can seek through the zip file (to rewrite the local header),
     * the whole file is transformed into a stored file:
     */

    // 整个文件都是未经压缩处理的文件，即stored file
    if (stored_len <= opt_lenb && eof && compressed_len == 0L && seekable()) {
        ...
        // 相比下一个if分支，它都不是以block形式组织数据，直接将数据原样输出
        copy_block(buf, (unsigned)stored_len, 0); /* without header */
        compressed_len = stored_len << 3;
        *file_method = STORED;
    } else if (stored_len+4 <= opt_lenb && buf != (char*)0) {
        // 4: LEN + NLEN
        // 当前block未经压缩，即00(no compress)
        send_bits((STORED_BLOCK<<1)+eof, 3);  /* send block type */
        compressed_len = (compressed_len + 3 + 7) & ~7L;
        compressed_len += (stored_len + 4) << 3;
        copy_block(buf, (unsigned)stored_len, 1); /* with header */
    } else if (static_lenb == opt_lenb) {
        // block使用Fixed Huffman codes编码
        send_bits((STATIC_TREES<<1)+eof, 3);
        compress_block((ct_data near *)static_ltree, (ct_data near *)static_dtree);
        compressed_len += 3 + static_len;
    } else {
        // block使用dynamic Huffman codes编码
        send_bits((DYN_TREES<<1)+eof, 3);
        send_all_trees(l_desc.max_code+1, d_desc.max_code+1, max_blindex+1);
        compress_block((ct_data near *)dyn_ltree, (ct_data near *)dyn_dtree);
        compressed_len += 3 + opt_len;
    }
    Assert (compressed_len == bits_sent, "bad compressed size");
    init_block();

    if (eof) {
        Assert (input_len == bytes_in, "bad input size");
        bi_windup();
        compressed_len += 7;  /* align on byte boundary */
    } else if (pad && (compressed_len % 8) != 0) {
        send_bits((STORED_BLOCK<<1)+eof, 3);  /* send block type */
        compressed_len = (compressed_len + 3 + 7) & ~7L;
        copy_block(buf, 0, 1); /* with header */
    }

    return compressed_len >> 3;
}

3.1 build_bl_tree首先调用scan_tree扫描literal & length、distance字符表的Run Length Encoding得到REL字符表的字符出现频次(bl_tree[m].Freq)。随后调用build_tree对REL字符表进行Huffman编码。并返回Huffman编码长度不为0的REL字符在RLE字符表中的最大索引max_blindex。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
local void scan_tree (tree, max_code)
    ct_data near *tree; /* the tree to be scanned */
    int max_code;       /* and its largest code of non zero frequency */
{
    int n;                     /* iterates over all tree elements */
    int prevlen = -1;          /* last emitted length */
    int curlen;                /* length of current code */
    int nextlen = tree[0].Len; /* length of next code */
    int count = 0;             /* repeat count of the current code */
    int max_count = 7;         /* max repeat count */
    int min_count = 4;         /* min repeat count */

    if (nextlen == 0) max_count = 138, min_count = 3;
    tree[max_code+1].Len = (ush)0xffff; /* guard */

    for (n = 0; n <= max_code; n++) {
        curlen = nextlen; nextlen = tree[n+1].Len;
        if (++count < max_count && curlen == nextlen) {
            continue;
        } else if (count < min_count) {
            bl_tree[curlen].Freq += count;
        } else if (curlen != 0) {
            if (curlen != prevlen) bl_tree[curlen].Freq++;
            bl_tree[REP_3_6].Freq++;
        } else if (count <= 10) {
            bl_tree[REPZ_3_10].Freq++;
        } else {
            bl_tree[REPZ_11_138].Freq++;
        }
        count = 0; prevlen = curlen;
        if (nextlen == 0) {
            max_count = 138, min_count = 3;
        } else if (curlen == nextlen) {
            max_count = 6, min_count = 3;
        } else {
            max_count = 7, min_count = 4;
        }
    }
}

local int build_bl_tree()
{
    int max_blindex;  /* index of last bit length code of non zero freq */

    /* Determine the bit length frequencies for literal and distance trees */
    scan_tree((ct_data near *)dyn_ltree, l_desc.max_code);
    scan_tree((ct_data near *)dyn_dtree, d_desc.max_code);

    /* Build the bit length tree: */
    build_tree((tree_desc near *)(&bl_desc));
    /* opt_len now includes the length of the tree representations, except
     * the lengths of the bit lengths codes and the 5+5+4 bits for the counts.
     */

    // max_blindex: REL字符表中Huffman编码长度不为0的最大字符在RLE字符表中的索引
    for (max_blindex = BL_CODES-1; max_blindex >= 3; max_blindex--) {
        if (bl_tree[bl_order[max_blindex]].Len != 0) break;
    }    
    /* Update opt_len to include the bit length tree and counts */
    opt_len += 3*(max_blindex+1) + 5+5+4;
    return max_blindex;
}

3.2 send_all_trees首先填充dynamic Huffman codes编码的block要求的头部bits，下表是dynamic Huffman codes编码的block格式。随后调用send_tree将literal & length字符表Huffman编码的REL表示以及distance字符表Huffman编码的REL表示输出到block中。

length Meaning
5bits HLIT(literal & length max code + 1) - 257
5bits HDIST(distance max code + 1) - 1
4bits HCLEN(REL max code index + 1) - 4
(HCLEN + 4) x 3 bits REL字符表的Huffman编码的code length sequence表示，每个code length以固定3bit表示
(HLIT + 257) 编码个数 literal & length字符表Huffman编码的REL表示
(HDIST + 1) 编码个数 distance字符表Huffman编码的REL表示
LZ77压缩数据使用literal&length字符表、distance字符表的Huffman编码
The literal/length symbol 256 (end of data) 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
local uch near bl_order[BL_CODES]
   = {16,17,18,0,8,7,9,6,10,5,11,4,12,3,13,2,14,1,15};

local void send_tree (tree, max_code)
    ct_data near *tree; /* the tree to be scanned */
    int max_code;       /* and its largest code of non zero frequency */
{
    int n;                     /* iterates over all tree elements */
    int prevlen = -1;          /* last emitted length */
    int curlen;                /* length of current code */
    int nextlen = tree[0].Len; /* length of next code */
    int count = 0;             /* repeat count of the current code */
    int max_count = 7;         /* max repeat count */
    int min_count = 4;         /* min repeat count */

    /* tree[max_code+1].Len = -1; */  /* guard already set */
    if (nextlen == 0) max_count = 138, min_count = 3;

    for (n = 0; n <= max_code; n++) {
        curlen = nextlen; nextlen = tree[n+1].Len;
        if (++count < max_count && curlen == nextlen) {
            continue;
        } else if (count < min_count) {
            // code length的重复没有达到最小重复次数要求，将code length以REL字符表中的(0-15)的Huffman编码输出
            do { send_code(curlen, bl_tree); } while (--count != 0);
        } else if (curlen != 0) {
            // 当前重复的code length和之前的code length不同，则先输出code length
            if (curlen != prevlen) {
                send_code(curlen, bl_tree); count--;
            }
            Assert(count >= 3 && count <= 6, " 3_6?");
            // 随后输出编码REP_3_6 Huffman编码，以及2bit的重复次数
            send_code(REP_3_6, bl_tree); send_bits(count-3, 2);
        } else if (count <= 10) {
            // code length 0重复3-10次，输出REPZ_3_10 Huffman编码，以及3bit的重复次数
            send_code(REPZ_3_10, bl_tree); send_bits(count-3, 3);
        } else {
             // code length 0重复11-128次，输出REPZ_11_138 Huffman编码，以及7bit的重复次数
            send_code(REPZ_11_138, bl_tree); send_bits(count-11, 7);
        }
        count = 0; prevlen = curlen;
        if (nextlen == 0) {
            max_count = 138, min_count = 3;
        } else if (curlen == nextlen) {
            max_count = 6, min_count = 3;
        } else {
            max_count = 7, min_count = 4;
        }
    }
}

local void send_all_trees(lcodes, dcodes, blcodes)
    int lcodes, dcodes, blcodes; /* number of codes for each tree */
{
    int rank;                    /* index in bl_order */
    // 存在至少长度为3的length编码；存在至少距离为2的distance编码；存在至少长度为为4的code length REL编码
    Assert (lcodes >= 257 && dcodes >= 1 && blcodes >= 4, "not enough codes");
    Assert (lcodes <= L_CODES && dcodes <= D_CODES && blcodes <= BL_CODES,
            "too many codes");
    // HLIT HDIST HCLEN
    send_bits(lcodes-257, 5); /* not +255 as stated in appnote.txt */
    send_bits(dcodes-1,   5);  
    send_bits(blcodes-4,  4); /* not -3 as stated in appnote.txt */
    // REL字符表Huffman编码的code length sequence表示
    for (rank = 0; rank < blcodes; rank++) {
        send_bits(bl_tree[bl_order[rank]].Len, 3);
    }    

    send_tree((ct_data near *)dyn_ltree, lcodes-1); /* send the literal tree */
    send_tree((ct_data near *)dyn_dtree, dcodes-1); /* send the distance tree */
}

3.3 compress_block对LZ77算法压缩的字符流进行Huffman编码。literal & length字符流保存在l_buf中，使用ltree中字符的Huffman编码进行编码，distance字符流保存在d_buf中，使用dtree中字符的Huffman编码进行编码。对字符流中所有字符Huffman编码完成后，加上END_BLOCK的Huffman编码，标志该block结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
local void compress_block(ltree, dtree)
    ct_data near *ltree; /* literal tree */
    ct_data near *dtree; /* distance tree */
{
    unsigned dist;      /* distance of matched string */
    int lc;             /* match length or unmatched char (if dist == 0) */
    unsigned lx = 0;    /* running index in l_buf */
    unsigned dx = 0;    /* running index in d_buf */
    unsigned fx = 0;    /* running index in flag_buf */
    uch flag = 0;       /* current flags */
    unsigned code;      /* the code to send */
    int extra;          /* number of extra bits to send */

    if (last_lit != 0) do {
        if ((lx & 7) == 0) flag = flag_buf[fx++];
        lc = l_buf[lx++];
        if ((flag & 1) == 0) {
            send_code(lc, ltree); /* send a literal byte */
            Tracecv(isgraph(lc), (stderr," '%c' ", lc));
        } else {
            /* Here, lc is the match length - MIN_MATCH */
            code = length_code[lc];
            send_code(code+LITERALS+1, ltree); /* send the length code */
            extra = extra_lbits[code];
            if (extra != 0) {
                lc -= base_length[code];
                send_bits(lc, extra);        /* send the extra length bits */
            }
            dist = d_buf[dx++];
            /* Here, dist is the match distance - 1 */
            code = d_code(dist);
            Assert (code < D_CODES, "bad d_code");

            send_code(code, dtree);       /* send the distance code */
            extra = extra_dbits[code];
            if (extra != 0) {
                dist -= base_dist[code];
                send_bits(dist, extra);   /* send the extra distance bits */
            }
        } /* literal or match pair ? */
        flag >>= 1;
    } while (lx < last_lit);
    // 使用ltree字符表的Huffman编码，编码END_BLOCK
    send_code(END_BLOCK, ltree);
}

以LZ77压缩的字符流a(3,4)cd(4,7)bef为例，相应的数值(字符使用ASCII编码表示)是97,3,4,99,100,4,7,98,101,102。实际存储在flag_buf和d_buf中的数据(见ct_tally的调用点)是97,3-3,4,99,100,4-3,7,98,101,102即97,0,4,99,100,1,7,98,101,102。下图展示了字符流在l_buf和d_buf中的存储：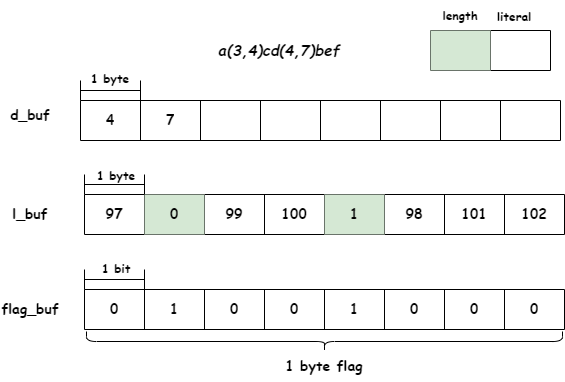

l_buf存储了literal和length - 3，以字节为单位存储。为了区分l_buf中的literal和length，使用flag_buf中的flagbit位区分。bit位为0，代表l_buf相应位置存储的是literal，若为1，则存储的是length。因此每处理完l_buf中的1个字符，flag要向右移动一位；每处理完l_buf中的8个字符，需要读取flag_buf中的下一个flag。

3.4 init_block为新的block做初始化工作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
local void init_block()
{
    int n; /* iterates over tree elements */

    // 初始化literal&length、distance、REL字符表字符的频次为0
    for (n = 0; n < L_CODES;  n++) dyn_ltree[n].Freq = 0; 
    for (n = 0; n < D_CODES;  n++) dyn_dtree[n].Freq = 0; 
    for (n = 0; n < BL_CODES; n++) bl_tree[n].Freq = 0; 

    dyn_ltree[END_BLOCK].Freq = 1; 
    // 初始化dynamic Huffman codes、static Huffman codes编码长度为0
    opt_len = static_len = 0L;
    // 将l_buf、d_buf、flag_buf的索引重置
    last_lit = last_dist = last_flags = 0; 
    flags = 0; flag_bit = 1; 
}

Summary

DEFLATE算法的Huffman编码的压缩过程可以用下图表示：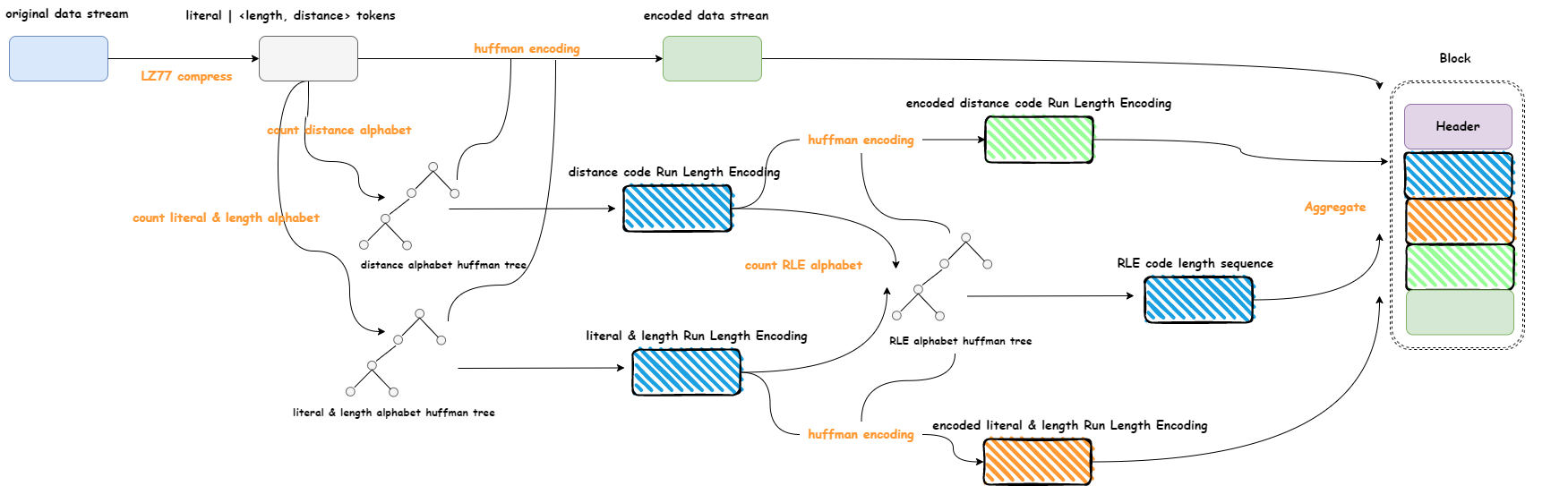

  1. 统计LZ77算法压缩数据流中literal、length出现的频次，构建literal & length字符表的Huffman树，并以RLE表示；同样得到distance字符表的Huffman编码的RLE表示
  2. 统计literal & length字符表、distance字符表Huffman编码的RLE表示中RLE字符出现的频次，构建RLE字符表的Huffman树，得到RLE字符表Huffman编码的code length sequence表示
  3. 将第2步的code length sequence以固定3bit编码输出到压缩数据流中；将第1步的2个RLE以第2步得到的REL字符表Huffman编码进行编码，并输出到压缩数据流中
  4. 将LZ77算法压缩数据流中的所有字符以第1步得到的两个字符表的Huffman编码进行编码，并输出到压缩数据流中
Related posts
Understanding gzip - LZ77gzip是一种压缩格式也是类Unix上的文件压缩/解压缩软件，通常指GNU计划的实现，此处gzip代表GNU zip。gz...

The post follows the Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0) License

Permalink:https://system-thoughts.github.io/posts/bbc4c4ba/

updated:Jan 18, 2023

gzip

deflate

Comments